Chaos Game in Processing

Yesterday, a video popped up on my Recommended YouTube playlist - titled “Chaos Game” by Numberphile

The Rules

Suppose we take a piece of paper and draw 3 dots. You can follow along if you wish, although this game is much easier when performed by a computer.

We also need a standard 6-sided dice as our random number generator. Since we have 6 sides and 3 dots, lets say (as is in the video) that numbers 1 and 2 belong to the first dot (lets call it A), 3 and 4 to the next dot (B) and lastly 5 and 6 to the last dot (C).

The rules are really simple. Pick a random position on the paper as your starting point and mark it with a small dot. Roll the dice and depending on the value, choose either dot A, B or C. Imagine a line between your starting point and the dot that was choosen. Mark a new starting position in the middle of that line. And roll the dice again. And draw another middle point, and so on and so on.

Repeat this enough times and you will start to see what the fuss is all about.

Once I saw (in the video) what the resulting image would become, I immediately opened Processing to write a simple sketch and try this idea out.

The game

To follow along, you will need Processing downloaded and installed on your system. Other than that you are all set.

First thing’s first, let’s create a new sketch. To get started we need at least 2 functions, setup and draw.

// global variables go up here

void setup() {
  size(600, 600);
  stroke(255);
  background(0);
}

void draw() {
    // pass
    return;
}

This will give us a 600 by 600 pixels wide window, with a black background and white points. We haven’t drawn any points so we just have a black background at this moment.

Since we will spend a lot of time dealing with points, let’s simplify our life and create a class called Point.

class Point {
  float x;
  float y;
  
  Point(float xx, float yy) {
    x = xx;
    y = yy;
  }
}

We will be dealing with many points so we should create some containers to store them. Add the following to the top of the file as global variables.

ArrayList<Point> points = new ArrayList<Point>();
ArrayList<Point> attractors = new ArrayList<Point>();

While we’re at it, let’s also create a quick helper function to add points to the attractors list.

void addAttractor(float x, float y) {
  attractors.add(new Point(x,y));
}

And add the following to the end of the setup function.

addAttractor(300,100);
addAttractor(100,500);
addAttractor(500,500);

Attractors are taken care of, so let’s think about our starting position. The reality is we can choose any coordinate we like, the result will always be the same after a few rolls of dice. Add the following as a global variable.

Point currentPoint = new Point(50,50);

In this case, coordinate 50,50 will do just fine.

Time to get down and dirty with the game. We first need a function that will perform a dice roll for us. Nothing fancy.

void performRoll() {
  
  float minRoll = 0;
  float maxRoll = attractors.size();
  
  float roll = random(minRoll, maxRoll);
  int index = ceil(roll) - 1;
  
  Point attractor = attractors.get(index);
  
  currentPoint = getMiddle(currentPoint, attractor);
  
  points.add(currentPoint);
}

We generate a random number between 0 and the number of attractors we have (in this case 3) and grab the attractor from the list.

We then call the function getMiddle (which we haven’t written yet) to calculate the middle point between our current position and the attractor we rolled.

Lastly, we replace the currentPoint with the newly calculated point and add it to our list of previously calculated points.

Before moving along, we should take care of this missing getMiddle function.

Point getMiddle(Point A, Point B) {
  float newX = (A.x + B.x) / 2;
  float newY = (A.y + B.y) / 2;
  return new Point(newX, newY);
}

Nothing fancy here, we take X and Y coordinates of both points, calculate middle coordinates and return an instance of Point on those coordinates.

It might also be useful to draw those attractors, so let’s take care of that in the function drawAttractors.

void drawAttractors() {
  strokeWeight(5);
  for (int i = 0; i < attractors.size(); i++) {
    Point attractor = attractors.get(i);
    point(attractor.x, attractor.y);
  }
  strokeWeight(1);
}

Here, we increase the stroke to 5 pixels, so they stand out from the crowd (it’s about to get very crowded) and call the built-in method of Processing called point() which takes a pair of X and Y positions and draws a square.

There is one final function we are missing, before we can assemble the program. And that is of course drawPoints, which draws all the points we have calculated by calling getMiddle.

void drawPoints() {
  for (int i = points.size() - 1; i >= 0; i--) {
    Point point = points.get(i);
    point(point.x,point.y);
  }
}

Again, nothing fancy here, just a loop that draws all the points in the points list.

It’s finally time to revisit draw function. Change it to the following:

void draw() { 
  performRoll();
  drawAttractors();
  drawPoints();
}

And that’s it. The way Processing works is by calling setup() just once in the beginning and then draw() on every frame. So each frame, we first calculate a new point and then draw the entire batch of points on the screen.

By definition, this program will slow down on every frame, since we are just accumulating more and more points and have to draw more of them every frame.

Output

We went through all this trouble to code a game, which looks to be a bunch of random rolls of dice. My first thought was that this process would eventually cover every possible position inside the triangle. Or something. Anything.

What followed next blew my mind. Take a look what happens after a few hundered interations.

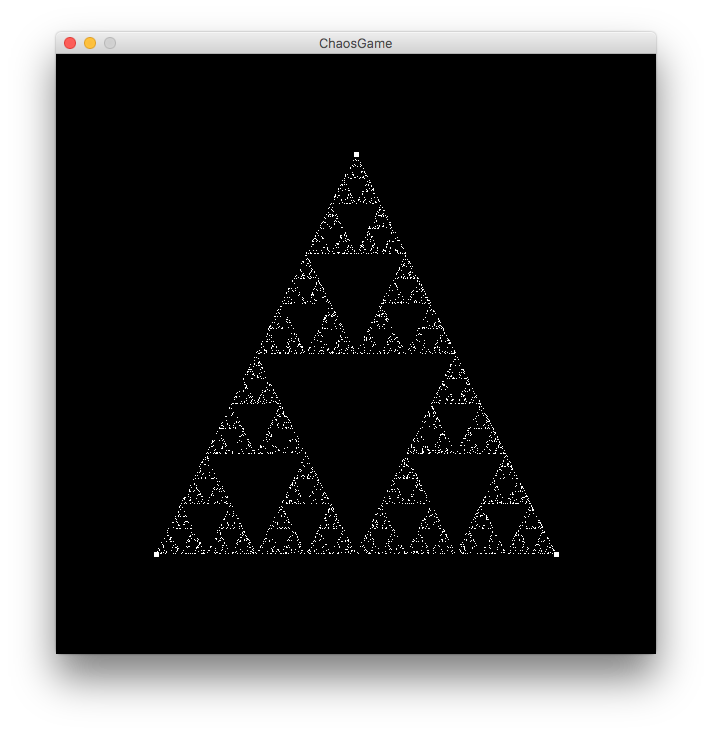
That’s right. A Sierpinski triangle. HOLY CHEEZEBALLS!

Entire code

In case you want to just copy and paste the entire code, here it is:

ArrayList<Point> points = new ArrayList<Point>();
ArrayList<Point> attractors = new ArrayList<Point>();

Point currentPoint = new Point(50,50);

void setup() {
  size(600, 600);
  stroke(255);
  background(0);
  
  addAttractor(300,100);
  addAttractor(100,500);
  addAttractor(500,500);
}

void addAttractor(float x, float y) {
  attractors.add(new Point(x,y));
}

void draw() { 
  performRoll();
  drawAttractors();
  drawPoints();
}

void drawPoints() {
  for (int i = points.size() - 1; i >= 0; i--) {
    Point point = points.get(i);
    point(point.x,point.y);
  }
}

void drawAttractors() {
  strokeWeight(5);
  for (int i = 0; i < attractors.size(); i++) {
    Point attractor = attractors.get(i);
    point(attractor.x, attractor.y);
  }
  strokeWeight(1);
}

void performRoll() {
  
  float minRoll = 0;
  float maxRoll = attractors.size();
  
  float roll = random(minRoll, maxRoll);
  int index = ceil(roll) - 1;
  
  Point attractor = attractors.get(index);
  
  currentPoint = getMiddle(currentPoint, attractor);
  
  points.add(currentPoint);
}

Point getMiddle(Point A, Point B) {
  float newX = (A.x + B.x) / 2;
  float newY = (A.y + B.y) / 2;
  return new Point(newX, newY);
}

class Point {
  float x;
  float y;
  
  Point(float xx, float yy) {
    x = xx;
    y = yy;
  }
}

Exercises

What would happen if instead of 3 attractors, we had 4 or 5? What about a hundred points forming a circle?

Random chaos

Let’s change our program a bit so that instead of using the 3 predefined attractors, we give it some random flair.

First, let’s define two new global variables.

int windowWidth = 600;
int windowHeight = 600;

Then create a new function to generate random attractors.

void addRandomAttractor() {
  float maxWidth = windowWidth * 0.8;
  float minWidth = windowWidth - maxWidth;
  float maxHeight = windowHeight * 0.8;
  float minHeight = windowHeight - maxHeight;
  
  float randomWidth = random(minWidth, maxWidth);
  float randomHeight = random(minHeight, maxHeight);
  
  addAttractor(randomWidth, randomHeight);
}

We should also modify the setup function and replace:

addAttractor(300,100);
addAttractor(100,500);
addAttractor(500,500);

with:

int maxAttractors = 5;

for (int i = 0; i < maxAttractors; i++) {
  addRandomAttractor();
}

This will create 5 attractors at random positions.